Prin intermediul acestei postări, veți învăța cum se calculează valorile și vectorii proprii ai unei matrici pătratice de ordinul 3, cu ajutorul unui exemplu concret. Există multe pagini unde puteți găsi teoria acestui subiect, însă este dificil de înțeles din teorie (unde se folosesc matrici de ordin n), cum se calculează în mod concret aceste elemente.
Mai întâi de toate, vreau să amintesc cum se calculează un determinant de ordinul 3, deoarece este necesar să efectuăm acest calcul asupra matricii, pentru a putea determina ceea ce ne interesează.
Determinantul unei matrici este un număr.
Considerăm următoarea matrice pătratică de ordinul 3, notată A:
Pentru a calcula determinantul acestei matrici, vom folosi regula triunghiului. Se observă în imaginea de mai jos că am marcat cele 2 diagonale ale matricii A, cu roșu am marcat diagonala principală, iar cu albastru diagonala secundară.
Pentru calcularea determinantului se procedează ca în imaginea de mai jos. Mai întâi înmulțim elementele de pe diagonala principală, apoi pe cele aferente acesteia (de deasupra, respectiv dedesubtul ei - se iau câte 2 elemente și colțul opus) și le punem cu semnul plus "+" în suma determinantului. Procedăm asemănător pentru diagonala secundară și elementele aferente ei, numai că pe acestea le vom pune cu minus "-" în suma determinantului.
Sper să înțelegeți mai bine modul cum înmulțim elementele matricii, în exemplul de mai jos.
În continuare vom lua un exemplu concret de matrice pe care vom calcula valorile și vectorii proprii.
Exemplu
Considerăm matricea următoare:
Rădăcinile polinomului le aflăm rezolvând ecuația det(A-λI3) = 0, după cum urmează :
Astfel: det(A-λI3) = 0 => (-4-λ) * (-1-λ) * (3-λ) = 0
Soluțiile ecuației de mai sus sunt:
-4-λ = 0 => λ1 = -4
-1-λ = 0 => λ2 = -1
3-λ = 0 => λ3 = 3
Deci, valorile proprii ale matricii A sunt: λ1 = -4, λ2 = -1 și λ3 = 3
Vectorii proprii ai matricii A
Se vor calcula vectorii proprii corespunzători celor 3 valori proprii ale matricii: λ1 = -4, λ2 = -1 și λ3 = 3. Pentru aflarea acestora rezolvăm câte o ecuație matriceală de forma (A-λI3) * X = 0, după cum urmează:
Pentru λ1 = -4 avem:
Astfel, ecuația (A-λI3) * X = 0 este:
Am notat deasupra primei matrice variabilele x1, x2 și x3, unde x1 corespunde primei coloane, x2 corespunde celei de-a doua coloană, iar x3 la cea de-a treia coloană.
Pentru rezolvarea ecuației, din această matrice de 3 linii pe 3 coloane, alegem una de 2 pe 2 (un minor de ordinul 2), care să aibă determinantul diferit de 0 (nenul). Variabila corespunzătoare coloanei rămase în afară, o vom nota cu t.
Notăm, x3 = t și avem ecuațiile:
2x1 + 3x2 = 0 (ec. 1)
x1 + 5x2 + 7t = 0 => x1 + 5x2 = -7t | *(-2) => -2x1 -10x2 = 14t (ec. 2)
Adunând ecuațiile 1 și 2, obținem: -7x2 = 14t => x2 = -2t
=> 2x1 + 3*(-2t) = 0 => 2x1 –
6t = 0 => 2x1 = 6t => x1 = 3t
Astfel, vectorul propriu X corespunzător primei valori proprii a matricii A este următorul:
Pentru λ2 = -1 avem:
Deci, ecuația (A-λI3) * X = 0 este:
Notăm, x3 = t și avem ecuațiile:
2x1 = 0 => x1 = 0
x1 + 5x2 + 4t = 0 => 0
+ 5x2 = -4t => x2 = -4/5 t
Astfel, vectorul propriu X corespunzător pentru a doua valoare proprie a matricii A este următorul:
Pentru λ3 = 3 avem:
Deci, ecuația (A-λI3) * X = 0 este:
Notăm, x3 = t și avem ecuațiile:
-7x1 = 0 => x1 = 0
2x1 -4x2 = 0 => 0 -4x2
= 0 => x2 = 0
Astfel, vectorul propriu X corespunzător celei de-a treia valori proprii a matricii A este următorul:
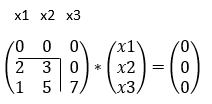
Niciun comentariu:
Trimiteți un comentariu