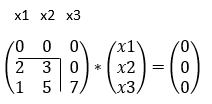În această postare voi prezenta alte 3 programe simple realizate cu Arduino Uno/Nano, câteva elemente de bază ale folosirii microcontrolerelor pe plăcuțe Arduino. Aceasta este o continuare a unei alte postări, în care am arătat cum se aprinde și stinge un LED, cum putem controla luminozitatea unui LED și modul în care afișăm mesaje pe Serial Monitor. Vă recomand să accesați postarea respectivă (deoarece vom folosi anumite noțini din ea pentru programele următoare), pe linkul următor :
Arduino Uno - Realizarea unui program
Prin intermediul primului program voi prezenta modul în care se face citirea digitală, în al doilea program vom folosi citirea analogică, iar în cel de-al treilea program voi arăta cum putem trimite comenzi prin intermediul ferestrei Serial Monitor.
1. Citirea digitală - conectarea unui buton la Arduino
În acest prim program vom folosi un buton (pushbutton), pe care îl conectăm la plăcuța Arduino. Vom mai conecta și un LED, care se va aprinde la apăsarea butonului, iar apoi se va stinge la următoarea apăsare. Butonul îl conectăm în felul următor: un picior al butonului la pinul de 5V, iar celălalt picior al butonului la un pin digital (de exemplu pinul 3) și printr-un rezistor de 10k ohmi la GND-ul plăcuței. Astfel, când butonul este apăsat, pe pinul digital vom avea tensiunea de 5V ( nivelul "1" logic), iar când nu este apăsat avem 0V, deci nivelul "0" logic.
Pentru determinarea nivelului logic vom folosi citirea digitală, prin instrucțiunea Arduino, digitalRead(pin); ,unde în loc de pin vom pune numărul pinul la care este conectat butonul.
În program vom folosi o variabilă în care citim starea butonului, o variabilă care să memoreze starea precedentă a butonului și o variabilă pentru starea ledului. Se vor folosi 2 LED-uri, cel existent pe plăcuță (conectat la pinul 13) și încă un LED conectat exterior, print-un rezistor la un pin digital al plăcuței (eu voi folosi în acest exemplu pinul 10).
 |
| Schema de conectare buton |
Programul folosit este următorul:
/*
Folosirea unui Pushbutton - citirea digitala
Conectarea butonului:
* un picior al butonului il punem la pinul de +5V al placutei
* al doilea picior il punem la pinul 3
* punem si un rezisor de 10K de la al doilea picior al butonului la GND
Cand butonul este apasat vom avea "1" logic, altfel avem "0" logic
Conectam un LED exterior. "+" LED-ului la pinul 10, iar minusul LED-ului il
conectam printr-un rezistor de 220 ohmi la GND
*/
int b = 0; // variabila pentru a citi starea butonului
int a=0, s=0; // alte variabile pentru memorarea anumitor informatii
void setup() {
pinMode(3, INPUT); // pinul la care este conectat butonul (folosit ca intrare)
pinMode(10, OUTPUT); // pin setat ca iesire (pinul la care conectam un LED)
pinMode(13, OUTPUT); // pinul 13 are un led conectat la el pe placuta Arduino
digitalWrite(10,LOW); // starea initiala a LED-ului (LOW = "0" logic = stins)
digitalWrite(13,LOW); // starea initiala a LED-ului (LOW = "0" logic = stins)
}
void loop() {
b = digitalRead(3); // se citeste starea butonului(apasat sau neapasat)
if (b == LOW) // daca butonul este neapasat, memoreaza acest lucru intr-o variabila
a=0; // memoram intr-o variabila ca pinul este pe nivelul "0" logic
if ((a==0) and (digitalRead(3)==HIGH)){ // daca starea precedenta este "0" si citirea actuala indica "1" logic(HIGH), va schimba starea LED-ului
if (s==0){ // verifica daca LED-ul este stins sau aprins
// daca LED-ul este stins:
digitalWrite(10, HIGH); // aprindem LED-ul de la pinul 10
digitalWrite(13, HIGH); // aprindem LED-ul de la pinul 13
s=1; // variabila pentru starea LED-ului
}
else{
// daca LED-ul este aprins:
digitalWrite(10, LOW); // stingem LED-ul de la pinul 10
digitalWrite(13, LOW); // stingem LED-ul de la pinul 13
s=0;
}
a=1; // atribuim valoarea 1 variabilei care memoreaza starea anterioara a butonului
}
delay(100); // asteptam 100 de ms(milisecunde) intre momentele in care citim starea butonului
}
Programul de mai sus pare puțin complicat, deoarece folosim o variabilă în care memorăm starea anterioară a butonului. Avantajul acestui program este acela că nu contează cât timp ținem apăsat butonul, la o apăsare fie scurtă, fie mai lungă, starea LED-urilor se schimbă o singură dată.
Un pushbutton poate fi folosit cu un program mai simplu, în care doar citim starea butonului și când aceasta este 1 logic să schimbăm starea LED-ului. Însă dacă intervalul de timp la care se face citirea este mare, este posibil să nu detecteze o apăsare mai scurtă, iar dacă intervalul de timp este prea mic se schimbă starea de mai multe ori la o singură apăsare.
Putem îmbunătății programul de mai sus, prin introducerea unei alte variabile, în care să memorăm numărul de apăsări, iar în funcție de acestă să efectuăm o anumită operație.
Am realizat montajul pe breadboard, cu un Arduino Nano, ca în imaginea de mai jos. LED-ul de pe plăcuță, de la pinul 13 se va aprinde/stinge simultan cu LED-ul conectat exterior la pinul 10, la o apăsare a butonului.
 |
| Montajul realizat pe breadboard + Arduino Nano |
 |
| Ledurile aprinse după apăsarea butonului |
2. Citirea analogică - folosirea unui fotorezistor
Prin acest program voi arăta cum putem afla nivelul de luminozitate într-o încăpere. Aceasta se va face destul de simplu prin folosirea unui fotorezistor pe care îl conectăm la plăcuța Arduino. Fotorezistorul este caracterizat de o rezistență care variază în funcție de nivelul de lumină. Vom conecta fotorezistorul la un pin cu funcție de intrare analogică (de exemplu A0) și vom face o citire analogică pe acest pin.
Schema de conectare a fotorezistorului este următoarea:
- un picior al fotorezistorului îl punem la pinul de 5V.
- al doilea picior al fotorezistorului îl punem la un pin cu funcție de intrare analogică, eu voi folosi pinul A0.
- de asemenea, mai este necesar să conectăm un rezistor de 10k ohmi, de la al doilea picior al fotorezistorului la un pin de GND al plăcuței.
 |
| Montajul realizat pe breadboard |
 |
| Fotorezistor |
Programul pe care îl vom folosi va afișa în fereastra Serial Monitor, la un anumit interval de timp valoarea citită de la fotorezistor. Această valoare va fi un număr întreg între 0 și 1023, unde 0 reprezintă întuneric beznă, iar o valoare apropiată de 1023 este echivalentă cu o luminozitate foarte puternică. Pe pini folosiți ca intrări analogice, vom citi un nivel de tensiune între 0V și 5V, care cu ajutorul unui convertor analog-digital, de pe plăcuța Arduino, va reprezenta acest nivel de tensiune cu o valoare numerică, în intervalul specificat mai sus (0 - 1023). Pentru a transforma valoarea numerică în tensiune se procedează astfel. Înmulțim cu 5 valoare citită, apoi împărțim la 1023 și obținem tensiunea citită pe pinul plăcuței.
Programul folosit este următorul:
/* Fotorezistor - citirea analogica
* Conectam un picior al fotorezistorului pe pinul de 5V
* Conectam al doilea picior al fotorezistorului la pinul A0
* De la al doilea picior al fotorezistorului mai ducem o rezistenta de 10k la GND
Vom afisa in fereastra Serial Monitor valoarea citita
*/
void setup() {
Serial.begin(9600); // initializam comunicatia seriala
Serial.println("Fotorezistor"); //mesaj de inceput
Serial.println(""); // rand liber
}
int v; // variabila in care facem citirea valorii
void loop() {
v = analogRead(A0); // citim valoarea tensiunii pe fotorezistor
Serial.print("Valoarea citita este: "); // afisam un mesaj fara a trece pe randul urmator
Serial.println(v); // afisam valoarea citita si mutam cursorul pe randul urmator
delay(2000); // asteptam 2 secunde pana la urmatoarea citire
}
Copiați codul în programul Arduino IDE și realizați montajul corespunzător. Selectați în meniul Tools tipul plăcuței Arduino folosită (Uno sau Nano), încărcați programul pe aceasta (Upload), apoi deschideți fereastra Serial Monitor și o să vă apară ca în imaginea de mai jos. Valoarea citită trebuie să fie aproximativ constantă. Dacă acoperiți cu ceva fotorezistorul, valoarea trebuie să se apropie de 0, iar dacă îl puneți într-un loc mai luminos, aceasta trebuie să fie în jur de 1000 (maximul este 1023).
3. Trimiterea de comenzi în fereastra Serial Monitor
În următorul program, vă voi prezenta modul în care citim și interpretăm mesaje prin intermediul ferestrei Serial Monitor a programului Arduino IDE. Pentru aceasta vom folosi schema de mai sus cu fotorezistorul, la care mai adăugăm un LED, sau putem folosi LED-ul conectat la pinul 13 de pe plăcuța Arduino. Când vom trimite comanda "LED ON" vom aprinde LED-ul, la comanda "LED OFF" vom stinge LED-ul, iar la comanda "citeste" vom afișa valoarea citită de la fotorezistor.
Puteți folosi și montajul de la punctul 1, din care se înlătură butonul și se adaugă fotorezistorul ca în schema prezentată la punctul 2. Dar pentru simplitate putem să folosim doar pinul 13.
Trimiterea de comenzi prin intermediul ferestrei Serial Monitor și interpretarea acestora se face în felul următor. Mai întâi verificăm dacă a fost trimis un mesaj (dacă există date în buffer), cu instrucțiunea if (Serial.available()>0){...}, apoi vom citi mesajul într-o variabilă de tip șir de caractere (String), cu instrucțiunea Serial.readString(). După ce am citit un mesaj, verificăm conținutul acestuia și în funcție de el vom realiza anumite instrucțiuni.
Programul folosit este următorul:
/* Trimiterea de comenzi - Serial Monitor
Avem conectat un fotorezistor astfel:
* Conectam un picior al fotorezistorului pe pinul de 5V
* Conectam al doilea picior al fotorezistorului la pinul A0
* De la al doilea picior al fotorezistorului mai ducem o rezistenta de 10k la GND
Vom citi in fereastra Serial Monitor un mesaj si vom aprinde/stinge un LED
sau vom afisa valoarea citita de la fotorezistor sau un mesaj de eroare
*/
void setup() {
pinMode(13, OUTPUT); // declarm pinul la care este conectat LED-ul ca iesire
digitalWrite(13, LOW); // starea initiala a pinului este LOW = LED stins
Serial.begin(9600); // initializam comunicatia seriala
Serial.println("Trimiterea comenzilor pe Serial Monitor"); //mesaj de inceput
Serial.println(""); // rand liber
Serial.println(""); // rand liber
}
String m; //variabila pentru citirea mesajului
void loop() {
if (Serial.available()>0){ // verificam daca exista date (un mesaj) in buffer
m=Serial.readString(); // citim mesajul din buffer intr-un string
// verificam mesajul
if ((m=="LED ON") || (m=="led on") || (m=="led ON")) {
digitalWrite(13, HIGH); // aprindem LED-ul de la pinul 13(ledul de pe placa Arduino)
Serial.println("LED aprins"); // afisam un mesaj de confirmare
}
else if ((m=="LED OFF") || (m=="led off") || (m=="led OFF")) {
digitalWrite(13, LOW); // stingem LED-ul de la pinul 13
Serial.println("LED stins"); // afisam un mesaj de confirmare
}
else if ((m=="citeste") || (m=="Citeste")){
Serial.print("Valoarea citita este: "); // afisam un mesaj fara a trece pe randul urmator
Serial.println(analogRead(A0)); // citim si afisam valoarea tensiuni pe fotorezistor
}
else Serial.println("Comanda necunoscuta"); // afisam un mesaj de eroare
}
else delay(100); // daca nu avem date asteptam 0,1 secunde pana la urmatoarea verificare a buffer-ului
}
Am folosit programul atât pe o plăcuță Arduino Uno, cât și pe o plăcuță Arduino Nano. În fereastra Serial Monitor trebuie să vă apară asemănător cu imaginile de mai jos, în funcție de comenzile (mesajele) trimise.
Dacă ați înțeles programele din această postare și din postarea precedentă, puteți încerca diverse combinații cu LED-uri, butoane, fereastra Serial Monitor și alte componente.
Mult succes!